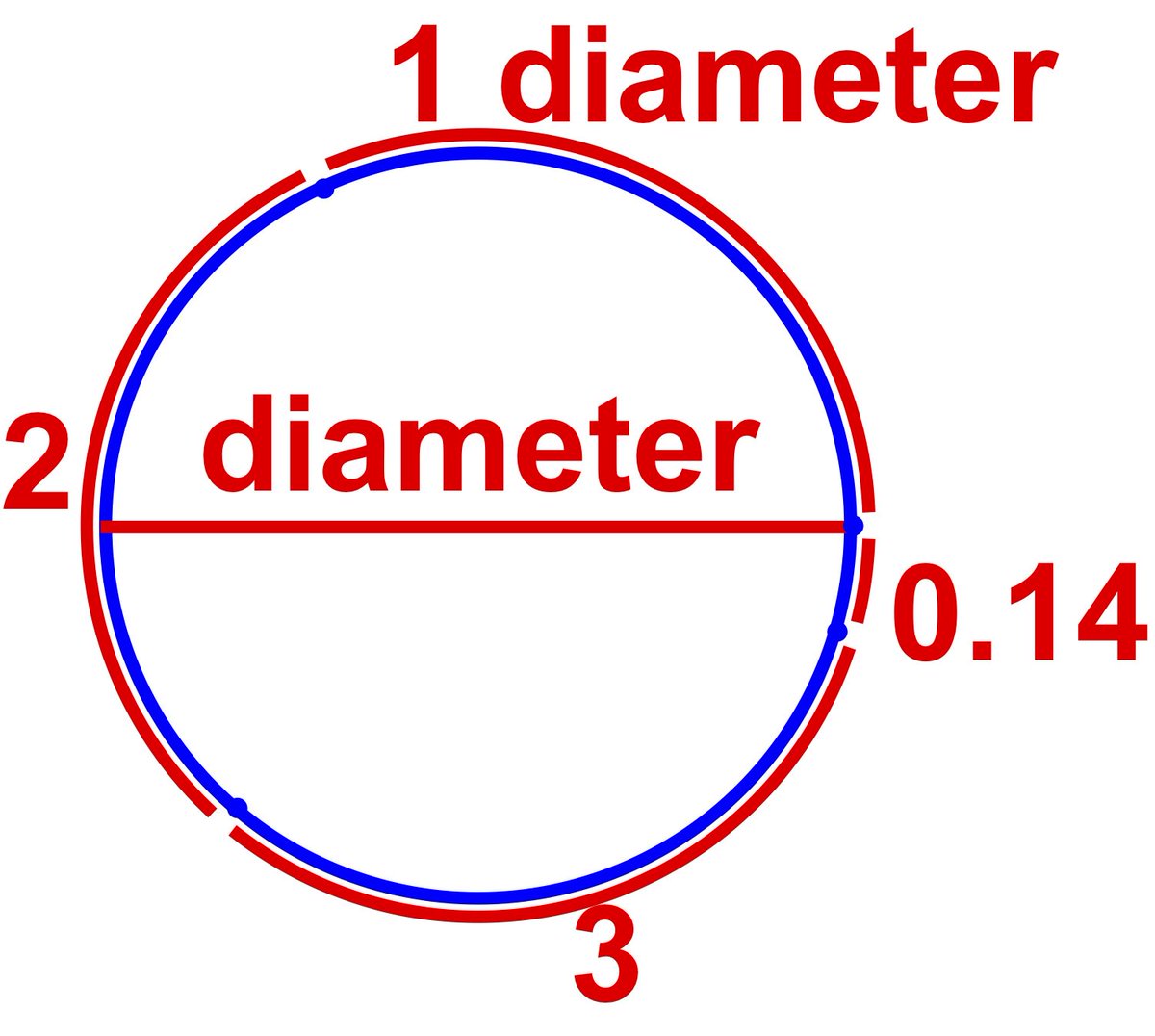
The number π ≈ 3.14, that is, the ratio of circumference to diameter of any circle, has continually captivated mankind since at least the ancient Babylonians four millennia ago.
It starts shortly after 300 BCE, when the great Greek geometer Euclid of Alexandria
3.14 ≈ π,
0.79 ≈ π/4,
0.52 ≈ π/6.
Area inside a circle of radius r = π r^2,
Volume inside a sphere of radius r = (4/3) π r^3.
It would have made Archimedes’s head spin to think about it, but today lots of real-world applications require
π^2/32≈31%
of a hypercube on its diameter, and in 10 dimensions, that proportion goes down to
π^5/122880≈0.25%
π^4/384 ≈ 25%
and in 24-D it is
π^12/479001600 ≈ 0.19%.
1/1+1/4+1/9+1/25+... ≈ 1.644934
What on earth do sums of inverse squares have to do with circles or spheres?!
(See the answer in this nice paper math.chalmers.se/~wastlund/Cosm… by Johan W¨astlund, on which this @3blue1brown video is based: )
1/1^4+1/2^4+1/3^4+1/4^4=1+1/16+1/81+1/256+...=π^4/90≈1.0823.
In fact, any such sum of reciprocals of even powers can be evaluated with π.
1/1^3+1/2^3+1/3^3+1/4^3...=1+1/8+1/27+1/64+1/125... ≈ 1.202.
Even armed with all our modern technological advances over the centuries and millennia, compelling this number to reveal itself remains as impenetrable today as in Euler’s time!