Thread by @hulme_oliver

What is ergodicity? ...and does it matter for human behavior?

In this paper we explain what it is,

why it constrains how people should make decisions when facing risk,

and we present (the first?) direct experimental evidence that it does matter.

Here is the pre-print, loosely summarised below.

arxiv.org/pdf/1906.04652…

(do tell me if this was done before, or somehow predicted by Aristotle).

Ergodicity is a foundational concept in physics.

An observable is ergodic if the average over its possible states at a fixed time (an expectation value) is the same as its average over time (a time average).

e.g. the velocity of gas molecules in a chamber is ergodic if...

averaging over all molecules at a given time (an expectation value),

yields the same answer as averaging a single molecule over an extended period of time (a time average).

In other words, ergodicity ensures an equality between the expectation value and the time average.

We ain't no gas molecules, so how is this relevant human behavior?

Ergodicity constrains how agents should compute averages when making decisions, because time averages are the only averages that individuals can expect to experience.

We (typically) cannot access averages that are computed over multiple agents or parallel universes.

Suppose we have a gamble that has additive dynamics. Win 5$ for heads, lose 4$ for tails.

Changes in wealth under this gamble are ergodic, so calculating the expectation value is informative of the time average growth rate of wealth.

To express in terms of utility: a linear utility function is optimal for additive dynamics because maximising changes in expected utility (i.e expectation value) acts to maximise the time average growth rate of wealth. We call this a time optimal utility function

Now consider a gamble with multiplicative dynamics.

Win 50% of your current wealth for heads, lose 40% of your current wealth for tails.

Changes in wealth now are non-ergodic, so calculating the expectation value is not informative of the time average growth rate of wealth.

(this exact gamble has a positive expectation value, but it has a negative time average growth rate. We call it the "Peters coin game" @ole_b_peters)

Now with multiplicative dynamics such as these, it is log utility that is time optimal, because maximising changes in expected utility maximises the time average growth rate of wealth.

In this framework, the utility function acts to transform wealth changes into an ergodic observable, which then gives you access to the time average, which to repeat, is (typically) the only average that individuals can access.

The big idea is that if we want to grow wealth over time, then this principle of time optimality can guide us as to how to modify our utility functions to maximise how fast our wealth grows over time.

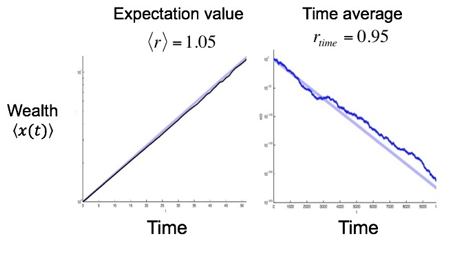
All ideas so far are from @ole_b_peters, Murray gell-mann + @alex_adamou.

Since most utility theories assume stable but idiosyncratic utility, whereas time optimality predicts specific utility functions for specific dynamics,...

...then the two classes of theory make different predictions for how people make choices.

We experimentally manipulated the ergodic properties of a simple gambling environment.

Subjects were endowed with lots of money, then they observed how fractal images caused this wealth to change.

They had to choose between different gambles comprised of these fractals.

On the additive day fractals caused additive changes in wealth. On multiplicative day, fractals caused multiplicative changes.

Via a Bayesian hierarchical model of isoelastic utility we estimated risk aversion parameters.

Estimating the risk aversion parameter separately for each dynamic, we could observe the distribution of risk aversions, and how they change when the dynamics change.

If subjects are indifferent to dynamics, then the distributions of risk aversion parameters should largely overlap.

If time optimal, they should shift from approximately linear utility to log utility, when ergodicity breaks in moving from additive to multiplicative dynamics.

As this figure shows, collapsing over subjects, there is a shift from near linear (0 on x axis) to to near log utility (1 on x axis).

Dotted lines indicate time optimal predictions.

Another way to visualise this is via a heatmap.

Time optimality predicts a clustering around the (0,1) coordinate where linear and log utility intersect.

Invariance to dynamics predicts a clustering around the diagonal.

We can see that the time optimal prediction is closer for each subject than the predictions of a dynamic-invariant utility, for all subjects.

We then directly compared prospect theory, isoelastic utility, and the time optimal model, via a Bayesian hierarchical latent mixture model.

In this small cohort at least (n=18), there is relatively strong evidence in favour of time optimality, over other models.

To sum up.

Ergodicity-breaking can exert strong and systematic effects on human behavior.

Switching from add- to multi- dynamics reliably increased risk aversion, which in most subjects tracked close to the levels that maximise the time average growth of wealth.

We show that these effects could not be adequately explained by two of the most popular models of utility in economics and psychology, and are better approximated by a null model of time optimality.

Credit first-foremost to @DavidMeder2 as 1st author, @RabeFinn who collected data and was patient throughout, @KoudahlM, Kris Madsen, Ray Dolan, Tobias Morville whose scepticism helped immensely, Hartwig Siebner for pushing us to be more ambitious + @DRCMR_MRI

Big thanks to Ole Peters, Alex Adamou, Mark Kirstein and Yonatan Berman for their enthusiastic expertise in helping us understand ergodicity

Shout out to the JASP course jasp-stats.org/workshops/ + Bayesian cognitive modelling course bayescourse.socsci.uva.nl, which we cannot recommend highly enough @EJWagenmakers, @richarddmorey @MdlBayes

We will be replicating this very soon via a registered report. We solicit collabs interested in testing over a much larger sample size. Particularly interested in adversarial collaborators who have substantive ideas for how to more severely discriminate between these theories.