Thread by @GaelVaroquaux

Comparing distributions: Kernels estimate good representations, l1 distances give good tests

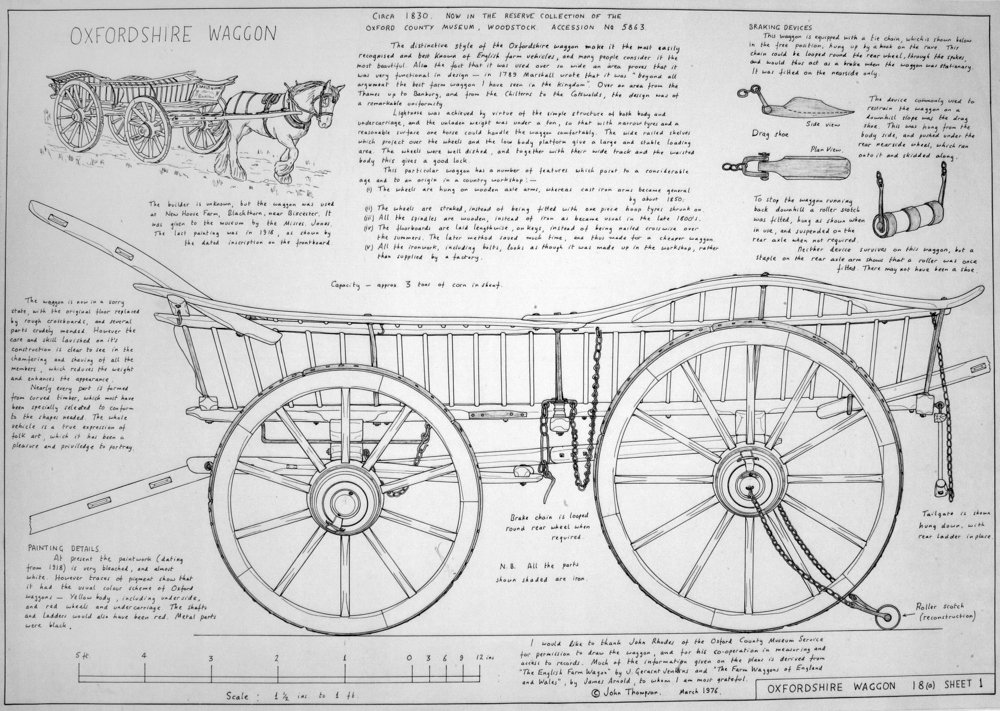
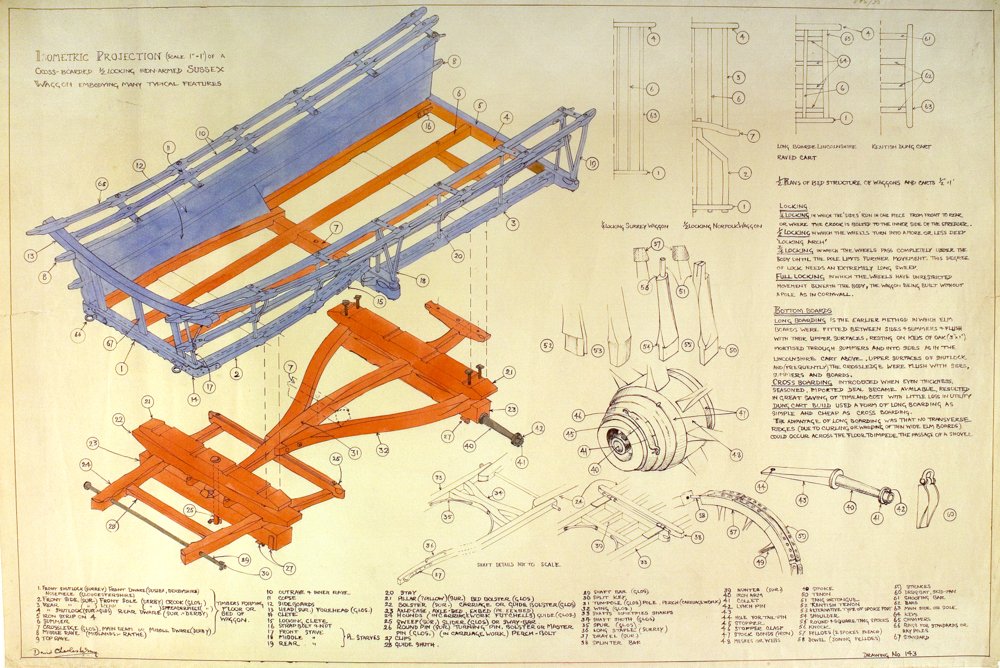
A simple summary of our #NeurIPS2019 work
gael-varoquaux.info/science/compar…

Given two set of observations, how to know if they are drawn from the same distribution? Short answer in the thread..

For instance, do McDonald’s and KFC use different logic to position restaurants? Difficult question! We have access to data points, but not the underlying generative mechanism, governed by marketing strategies.

To capture the information in the spatial proximity of data points, kernel mean embeddings are useful. They are intuitively related to Kernel Density Estimates

Metrics between distributions built from differences of their kernel mean embeddings can capture when probability measures "weakly converge": they give close probabilities to events that are close in measurement space, and not only to the exact same events (restaurants next door)

An example where weak convergence is important is for neighboring Diracs: comparing only probabilities at the same point gives infinite distance between the distributions if they are not exactly equal.

Kernel capture weak convergence by representing measurement neighborhoods.

We characterize a family of metrics between distributions defined via Lp distances between their kernel representatives.

With common kernels, the difference between representatives is dense. As a result, the l1 norm captures best their differences.

Intuitively, dense representations lie on diagonals while sparse ones are aligned with the coordinate axes. l1 norms make best the difference.

We show that l1 differences of distribution representations lead to good two-sample tests, with good power and closed-form null.

For fast and performant tests, instead of computing full sums over the measurement domains, the metrics can be sampled at a few locations Tj, random or optimized.

More in the full post, that itself links to the paper
gael-varoquaux.info/science/compar…

This framework builds upon solid mathematical foundations (RKHS), fast testing procedures, and a line of results that originated from MMD, maximum mean discrepancy.

For those at #NeurIPS2019 , @ArthurGretton, @wittawatj and D Sutherland give on Monday a tutorial on these concepts nips.cc/Conferences/20…

@ScetbonM presents this specific work on Thur with a spotlight at 4:55pm and after during the poster reception
nips.cc/Conferences/20…