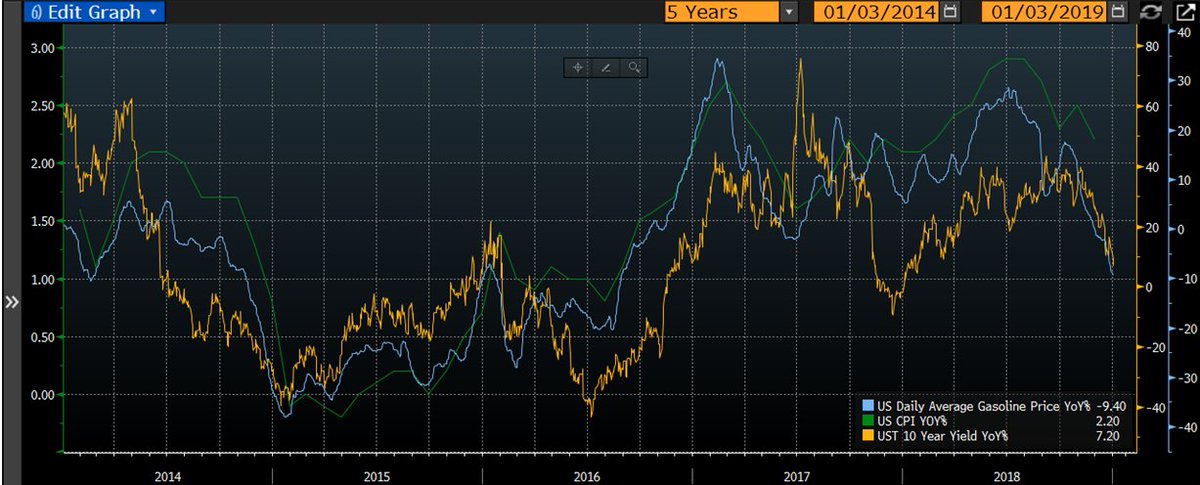
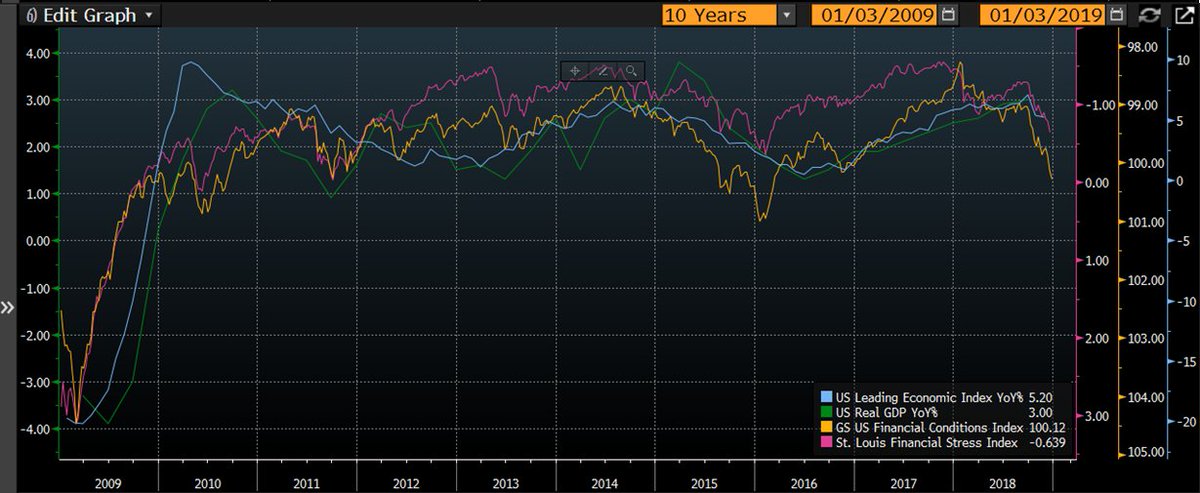
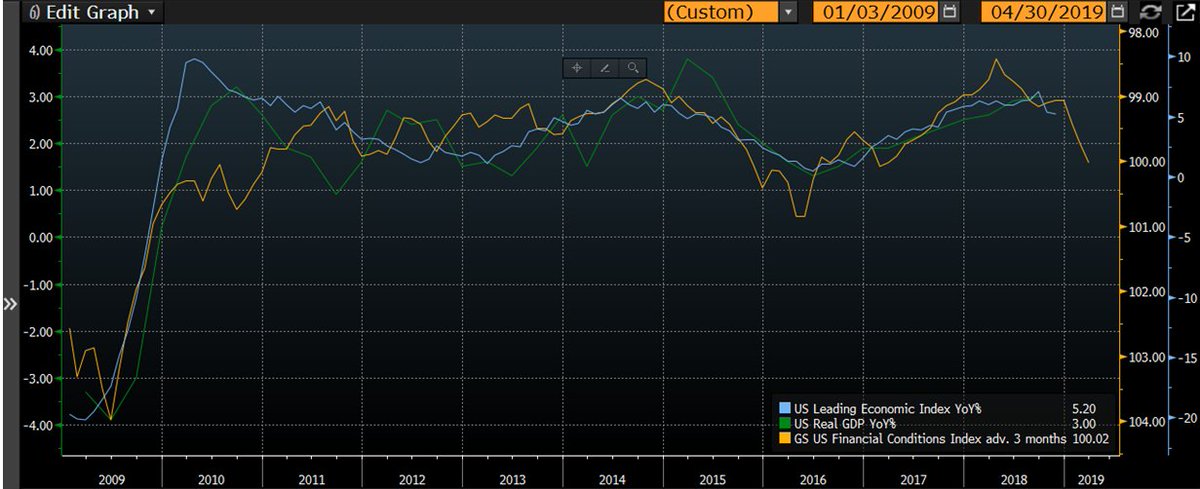
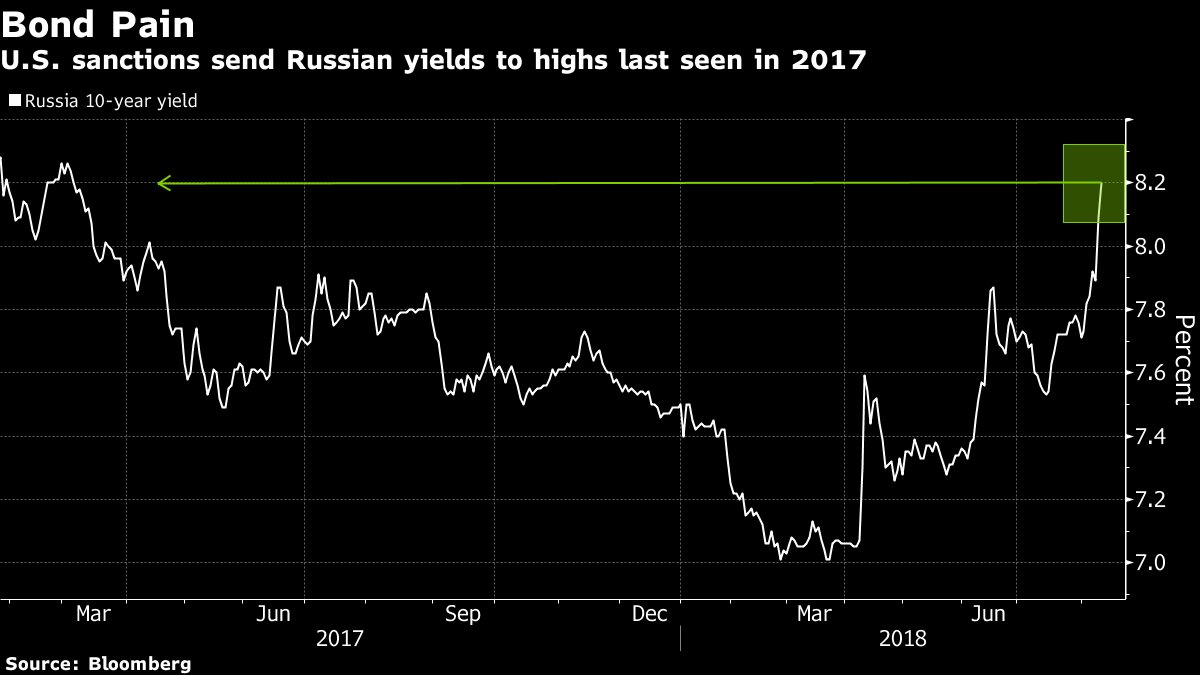
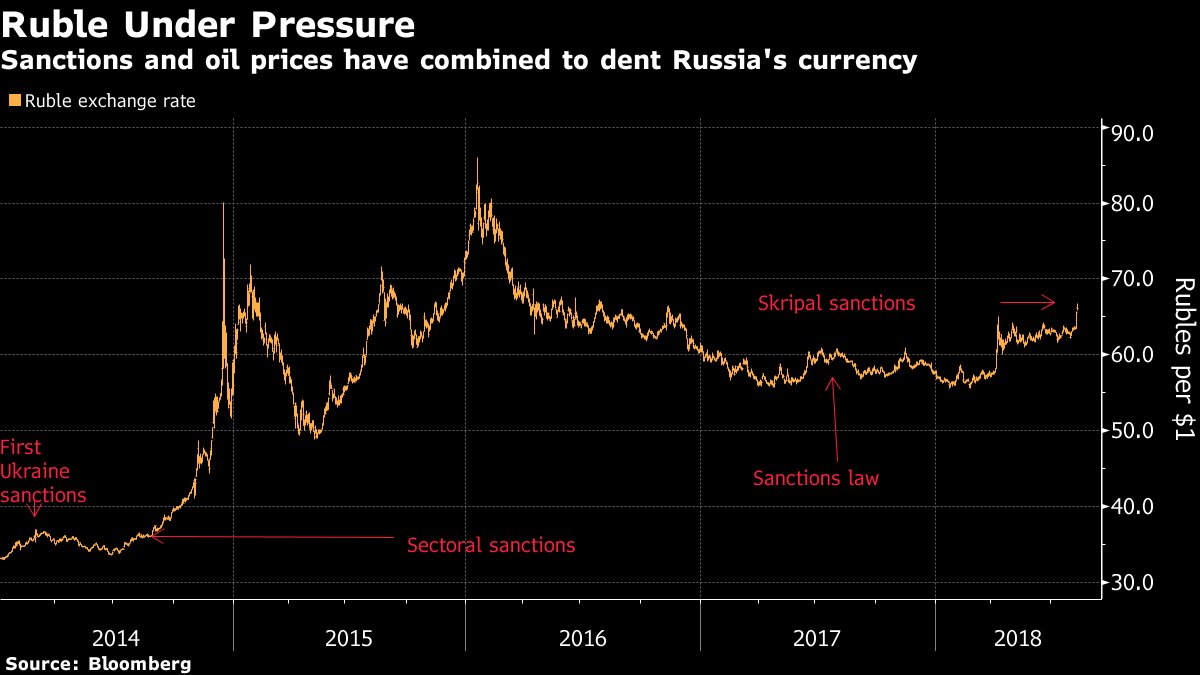
Nature approaches Ideals, but never quite reaches them.
The curve narrows towards the asymptope but never quite touches it.
If it does, it becomes tangential and the wave collapses. 1/
laetusinpraesens.org/docs80s/80vect…

cosmometry.net/the-torus---dy…



thoughtco.com/butterflies-gr…
rand.org/pubs/authors/n…
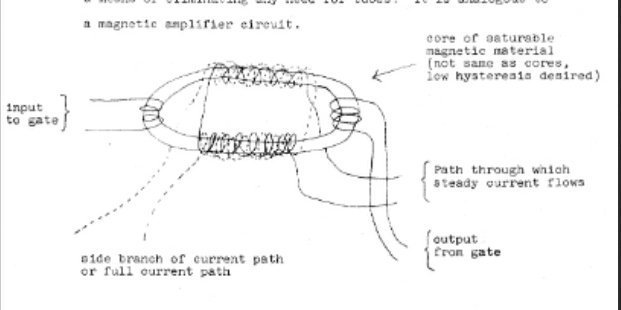
Nash utilized Langrangian Scalers in his Interesting Equation. The crown Jewel of his work.
H/T (@FX_Training_Grp) for the image.
Nash essentially said that the "inflation postulate" of Keynesian economics was similar to the the problem of Euclid's 5th postulate in Geometry.
What is interesting is that in topology (A field of mathematics central in Nash's work) both a dognut and a coffee mug are topologically equivalent.
In other words, central banks set out to make donuts, but often end up with coffee mugs.
Essentially, the snake eating its own tail.
Interesting that we use the analogue "inflation" in the sense of air filling a tire, to describe this.
It is actually quite applicable.