Thread by @wtgowers

The Cantor set is the set of all real numbers between 0 and 1 that have just 0s and 1s in their ternary expansion (i.e., no 2s). It is what you get if you continue this process of "removing the middle third" to infinity.

That image, by the way, was by Thefrettinghand at English Wikibooks, CC BY-SA 2.5, commons.wikimedia.org/w/index.php?cu…

On a different topic, an algebraic number is any number that is a root of some polynomial with integer coefficients. (A simple example is the square root of 2, since that is a root of the polynomial x^2-2.)

Now for a little problem: can every real number be written as the sum of an algebraic number and a number in the Cantor set? If you know about the right mathematics, you'll find this a very easy question. If you don't, read on for the answer!

A famous fact about the Cantor set is that it is large in one sense and small in another (in fact, small in at least two others, but that will have to wait for another thread). The sense in which it is large is that it is uncountable. That's because every number ... 5/

in the Cantor set corresponds to an infinite sequence of 0s and 1s, and there are uncountably many of those, as an easy diagonal argument shows.

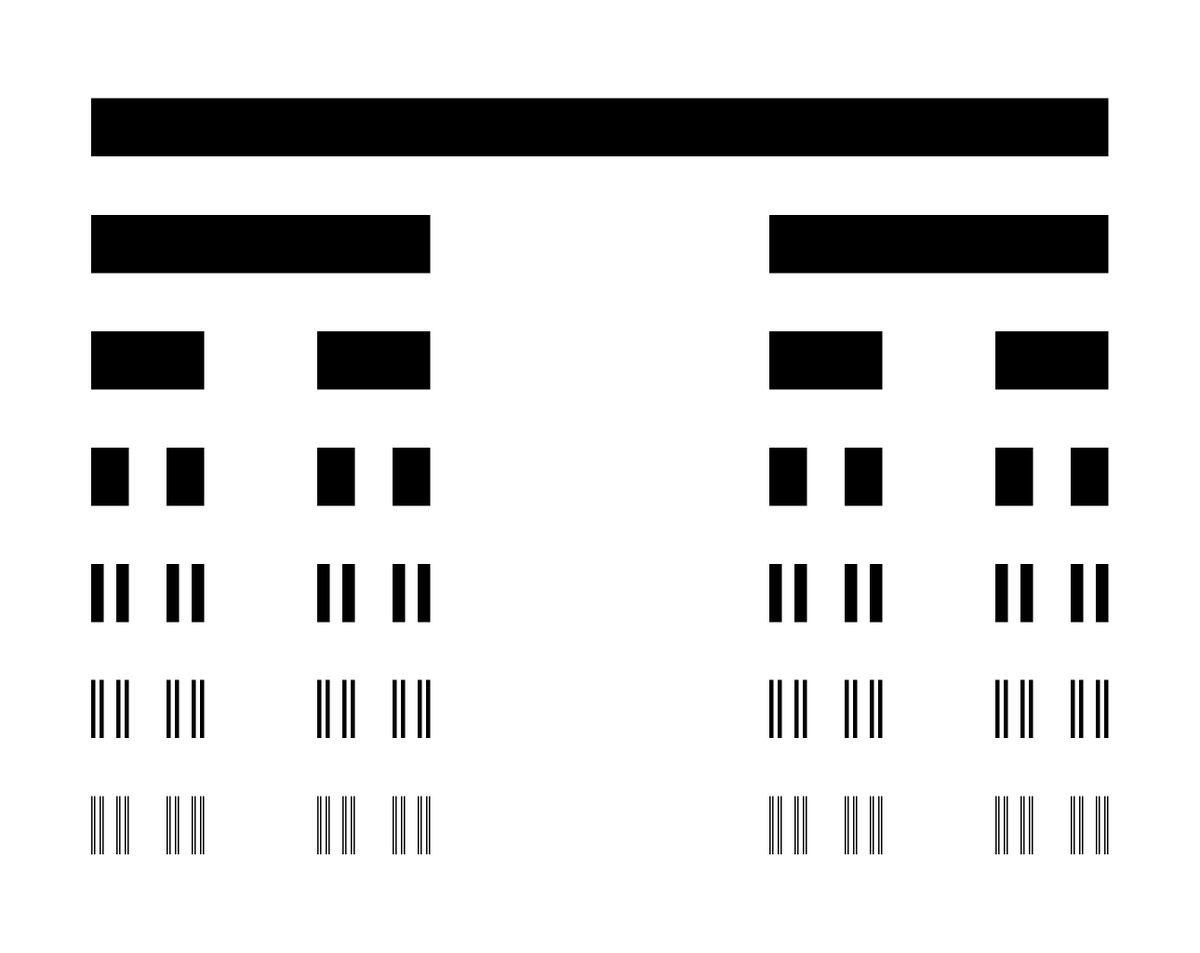
To see why it is small, let's think about how we might try to assign a "length" to the Cantor set. 6/

It's difficult to say immediately what we would mean by the length of such a complicated set, but we can think about some properties that any reasonable notion of length ought to have. One obvious one is that the length of an interval [a,b] should be b-a. 7/

Another is that the length of the union of two disjoint sets, one of length r and the other of length s, should be r+s.

And a third is that if A is a subset of B, and both sets have lengths, then the length of A should be at most the length of B. 8/

And here we're in luck -- just those properties are enough to show that the only possible length we can assign to the Cantor set is zero! To see why, note that the Cantor set is contained in the interval [0,1], so must have length at most 1. 9/

But it is also contained in the union of the intervals [0,1/3] and [2/3,1] so ... oh damn, I've just realized I messed up the definition of the Cantor set. It's numbers with just 0s and 2s in their ternary expansions. So it's 1s that are forbidden.

Coming back to this tweet to say that I meant to say that the allowed digits are 0 and 2 rather than 0 and 1. Apologies for this slip.

Anyway, it's contained in the union of those two intervals, so has length at most 1/3+1/3=2/3. Similarly, by looking at the next iteration we see that it has length at most 4/9, and in general it has length at most (2/3)^n for any n you choose. So it must have length 0. 11/

One might expect sets of length zero to be small, and there is an important fact that justifies that expectation, which is that a union of countably many sets of length zero cannot contain an interval of positive length. 12/

A key step in the proof is the following statement: that if you have a union of intervals I_1, I_2, I_3, ... with I_n having length a_n, then it cannot contain an interval of length greater than a_1+a_2+a_3+... 13/

That's not too hard to prove if you just have finitely many intervals, but it's a bit trickier if you have a countably infinite number. To get an idea of why, observe that whatever the lengths of the intervals, you can make sure that the union contains all the rationals. 14/

A quick sketch. If J is the interval you are trying to cover, let J_n be the set you get by removing all points from sets U_1,...,U_n, where U_j is an open interval that's very slightly bigger than I_j and the lengths of the U_j still add up to less than that of J. 15/

Then J contains J_1 contains J_2 contains J_3 etc. etc. and all the sets J_n are closed. They are also non-empty (by the result for finite unions of intervals). So by a basic result in analysis, they intersect, giving us a point in J not contained in any I_n. 16/

When do we say that a set has length zero? It's slightly more general than what we did for the Cantor set. A set A has length zero if for every c>0 we can cover A by a union of countably many intervals with total length at most c. 17/

For the Cantor set I could use finitely many intervals, but that isn't always the case. For example, the set of rational numbers (or indeed any other countable set) has length zero, but to show that you need to use infinitely many intervals. 18/

Using the lemma I sketched above, one can show that a union of countably many sets of length, or "measure" at is usually known, zero has length zero. And also that an interval [a,b] with a<b does *not* have length zero. 19/

And now the solution to the puzzle. Let the algebraic numbers be a_1, a_2, a_3, ... and let C be the Cantor set. Write a_n+C for all numbers of the form a_n+x with x in C. Then all the sets a_n+C have length zero, and there are countably many of them. 20/

Therefore, their union has length zero, so it isn't the set of all real numbers. But a real number not belonging to their union is not the sum of an algebraic number and an element of the Cantor set. 21/

The general message here is that we have another notion of smallness -- having length zero -- and it is *useful*. If you dispute that it is useful, can you find for me an example of a real number that isn't the sum of an algebraic number and an element of the Cantor set? 22/

Which brings me to a second general message: this is a nice example of an existence proof (of such a real number) that doesn't supply you with an example of the object shown to exist. Smallness notions are often useful in such proofs. 23/

Cantor's proof of the existence of transcendental numbers is another (famous) example.

I'd better end this thread as it's got pretty long. 24/24