Ini adalah Thread.
Dalam bahasa yang senang, sebuah matra ialah darjah kebebasan. Hal ini bertepatan dengan maksud "dimension" yang lain seperti "dimensional analysis".
(Matra lebih spesifik kepada sistem koordinat)
Berapa banyak arah yang aku boleh bergerak?
Contoh sistem bermatra-1 ialah sistem nombor. Kita hanya boleh kira ke arah positif-negatif (depan-belakang). Boleh ke kira arah lain?
Tak boleh. Sebab Barat Daya boleh juga disebut sebagai "sedikit Barat dan sedikit Selatan"
Begitu juga dengan Timur Laut = sedikit Timur dan sedikit Utara.
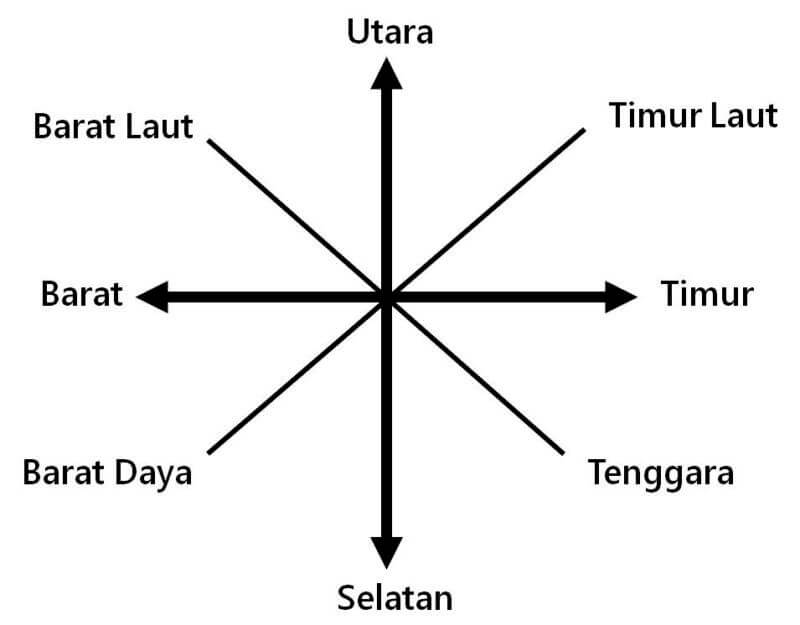
Kunci untuk menentukan arah matra baru ialah "Bolehkah pasangan arah ini diwakili dengan sistem arah yang sedia ada?"
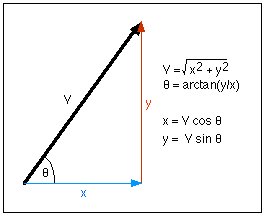
Adakah ia menjawab soalan tadi? Ya.
Macam mana kita nak bagitahu dia terbang naik atas kalau kita hanya kenal depan-belakang, kiri-kanan?

Tapi bagaimana pula dengan matra-4?
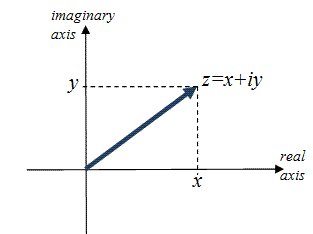
Tak mengapa. Pasangan arah apa itu tak penting, sebab yang penting, ada arah baru. Maka aku akan panggil arah baru ini pasangan khayalan.
Macam yang aku kata, apa itu arah baru dalam matra-4 ini tak penting, yang penting ialah kewujudan arah baru ini.
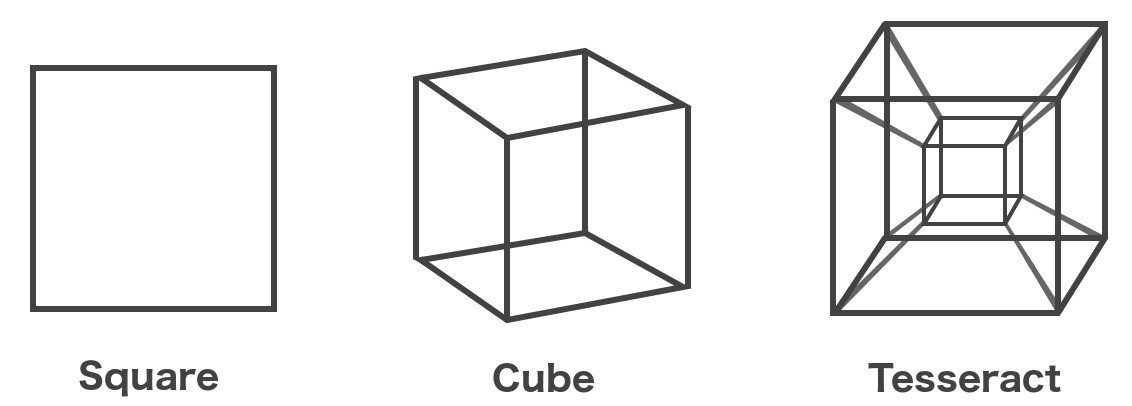
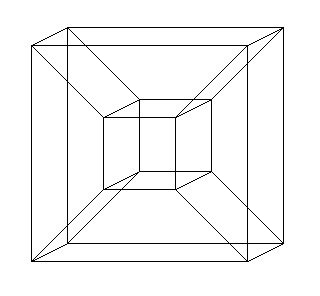
Persoalan itu sama seperti: Apa yang akan dapat dilihat oleh makhluk bermatra-2 kalau jasad bermatra-3 merentasi kertas bermatra-2?
Makhluk bermatra-2 seperti kotak dan segitiga, akan hanya boleh melihat keratan-keratan sebuah sfera. Keratan itu akan berubah saiz jika sfera itu naik-turun dalam arah yang tak dikenali sang kotak itu.

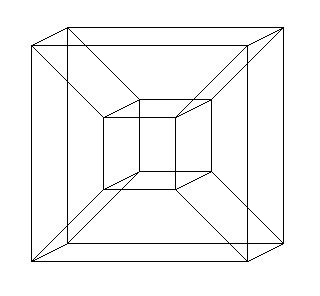
Secara intuitifnya, kita tahu kotak kecil tu maknanya ia jauh daripada kita berbading yang kotak besar itu.
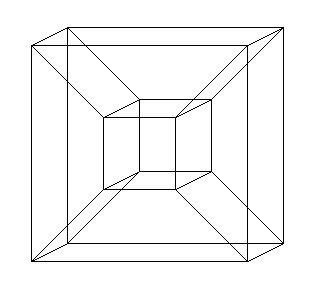
Kita akan nampak seperti kotak kecil itu menjadi besar dan kotak besar akan menjadi kecil.
Dia ada menyentuh pasal satu lagi jasad bermatra-4 yang menarik iaitu Botol Klein.