Thread by @KarenCampe

@von_Oy @anniek_p @Simon_Gregg @becky_k_warren @Trianglemancsd Here's my thinking:
Imagine not round table. There are 6 possibilities if A first, thus 6x4 total.

But ABCD on round same as BCDA, CDAB, DABC. So 24/4=6 ways. Also same as each of those reversed. So 6/2=3 ways.

ABCD, ABDC, ADBC in each, everyone has 2 unique neighbors.

@von_Oy @anniek_p @Simon_Gregg @becky_k_warren @Trianglemancsd For 5 people, there are 12 ways.
120 total orders if NOT round. /2 for reverses=60. /5 because if A first same as if any of other 4 first. So 12.

A next to BE can happen 2 ways
A next to BD same
A next to BC same, etc 3 more groups.

@von_Oy @anniek_p @Simon_Gregg @becky_k_warren @Trianglemancsd So my method would get me to 60 ways for a 6 person table.
6!=720
720/2=360 for reverses
360/6 because ABCDEF same as any other starting point when round loop.

@Trianglemancsd @von_Oy what do you think?

@von_Oy @anniek_p @Simon_Gregg @becky_k_warren @Trianglemancsd Or by pairing, A next to 5*4/2 possible pairs = 10 pairs.
Leaves 3 other table-mates, so 3! ways to arrange them.
10*6=60.
💥

@von_Oy @anniek_p @Simon_Gregg @becky_k_warren @Trianglemancsd OK, here is the info from Wolfram MathWorld. A circular permutation of n items is (n-1)!
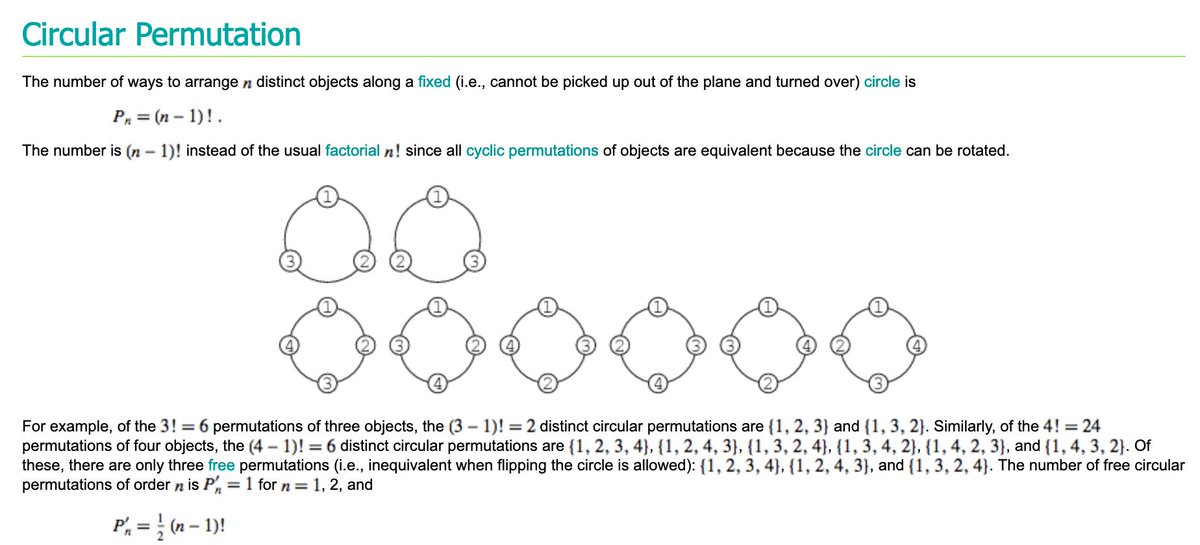
Our scenario allows "flipping the circle" meaning that 1st and 6th image below are equivalent, so number of distinct ways=1/2*(n-1)!