Thread by @fgrosshans

Now at #QuPa (at @InHenriPoincare) Carlo Maria Scandolo from @CompSciOxford on “Microcanonical thermodynamics in general physical theories”
#LTQI

@InHenriPoincare @CompSciOxford Carlo MAria Scandolo’s use the tools of resource theories, were some resources are free and others are costly.
Free resources induce a preorder: A more valuable then B if A –free→ B.
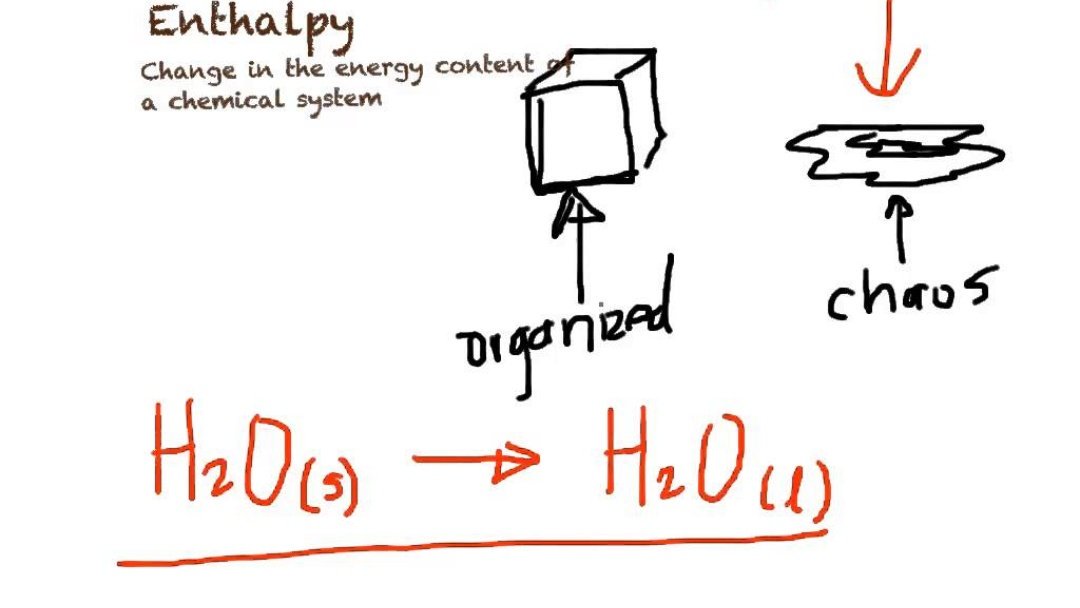
It describes allowed thermodynamics transitions
#LTQI #QuPa

@InHenriPoincare @CompSciOxford Carlo Maria Scandolo: A test is a collection of porcesses {C_i} with input A and B. A—[{C_i}]—B
Channel=deterministic test. Some are reversible.
State=test with no input
Observation test: test with no outputs
#LTQI #QuPa

Carlo Maria Scandolo then use this to construct circuits #LTQI #QuPa

Carlo MAria Scandolo: This general frameworks of operational-probabilistic theories (OPTs) is more generic than quantum mechanics. It contains stranger theories. #LTQI #QuPa

Carlo Maria Scandolo: Look at the microcanonical states, where all allowed microstates are equally probable.
Microstate=deterministic pure state.
Ideally χ=∫ψ dψ. χ should be unique and invariant under reversible dynamic.
#LTQI #QuPa

Carlo Maria Scandolo: χ exists in finite dimensions (from Haar Measure)
Theorem: χ is unique iff the action of reversible channels on deterministic pure states is transitive.
∀pair ψ, ψ', ∃reversible channel U s.t. ψ'=Uψ.
#QuPa #LTQI

Carlo MAria Scandolo: Reversible transformations are symmetries of the state space. E.g. ∄χ on the half disk, but it exists on the square (it’s at the centre)
#LTQI #QuPa

Carlo Maria Scandolo: It’s natural to set the χ of a composite system to be the compositionof microcanonical systems χAB=χA⊗χB
#LTQI #QuPa

Carlo Maria Scandolo: Noisy operations are generated by
1. prepare χ
2. apply reversible evolution
3. discard channels
#LTQI #QuPa

Carlo MAria Scandolo: There is also RaRe (Random reversible channels),
and the more generic unital channels mapping χA to χB
Noisy⊆Unital and RaRe⊆Unital
#LTQI #QuPa

Carlo Maria Scandolo look at sharp theories with purifications, where every pure state can be obtained (¿) via reversible operations (?)
#LTQI #QuPa

Carlo Maria Scandolo: These theories have following axioms:
causality,
purity preservation (composition of pure transformations is pure)
Pure Sharpness (∀system, ∃pure effect occuring with prob 1 on some state ρ)
...
#LTQI #QuPa

Carlo MAria Scandolo:
LAst axiom:
Purification (all state can be purified, aull purifcation ar equivialet upto reversible operation on purifying system)
#LTQI #QuPa

Carlo Maria Scandolo: Sharp theories with purification have a well defined microcanoncal state. All states are diagonalizable.
We have the following inclusion:
RaRe ⊆ Noisy ⊆ Unital

⇒RaRe convertibility is the harder to satisfy
#LTQI #QuPa

Carlo Maria Scandolo: Do eigenvalue of state tell anything about state convertibility? In classical & quantum theory, majorization plays an important role: ρ→σ if Sp(ρ)≻Sp(σ).
Almost the case, but majorization is not sufficient for RaRe channels (∃ counterexample)
#LTQI #QuPa

Carlo Maria Scandolo: An additional axiom (unrestricted reversibility) is necessary and sufficient to link majorization with eigenvalues.
But this leads to theories very close to quantum mechanics
#LTQI #QuPa

Carlo MAria Scandolo’s paper, arXiv:1608.04459 arxiv.org/abs/1608.04459 #LTQI #QuPa