same as saying that those patients who live until they respond survive longer than those who do not.
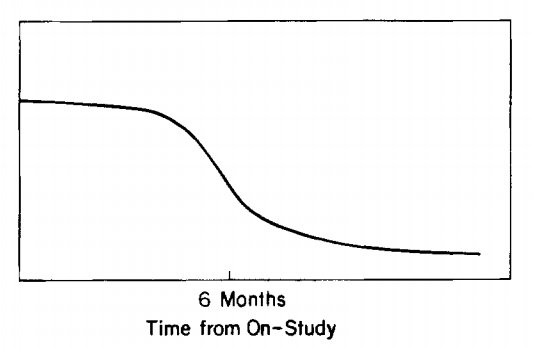
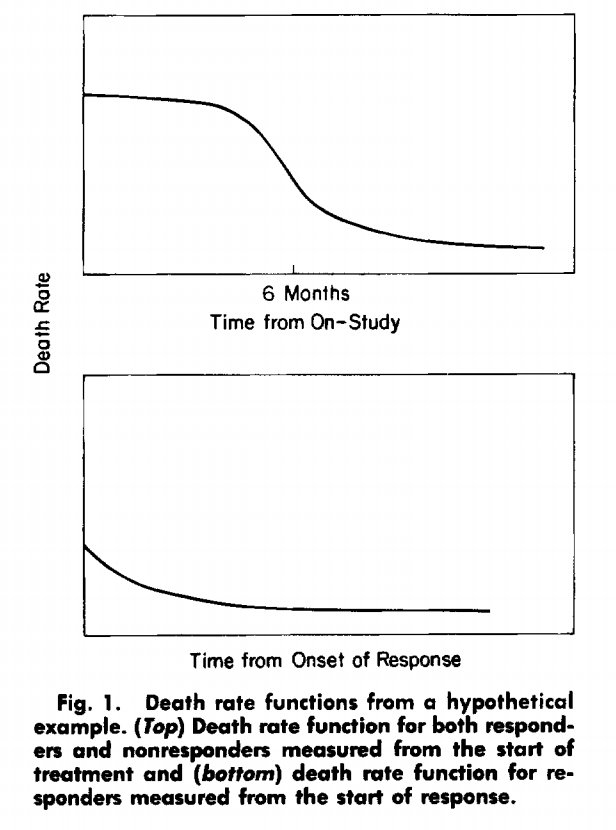
as defined at the landmark time is merely due to random variations or is statistically significant.
First, make sure the usual and modification methods of calculating survival are not used. The results are biased, the statistical test of significance is invalid, and the conclusions are misleading.




