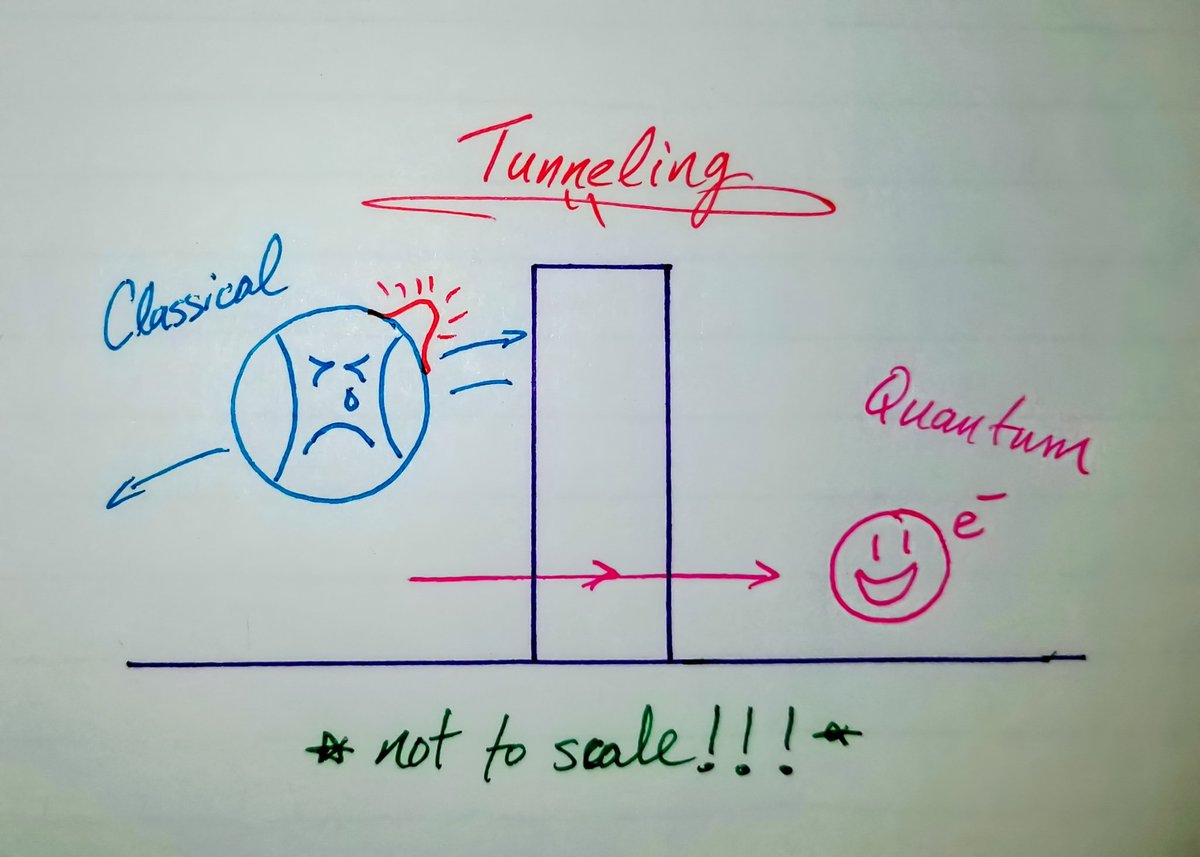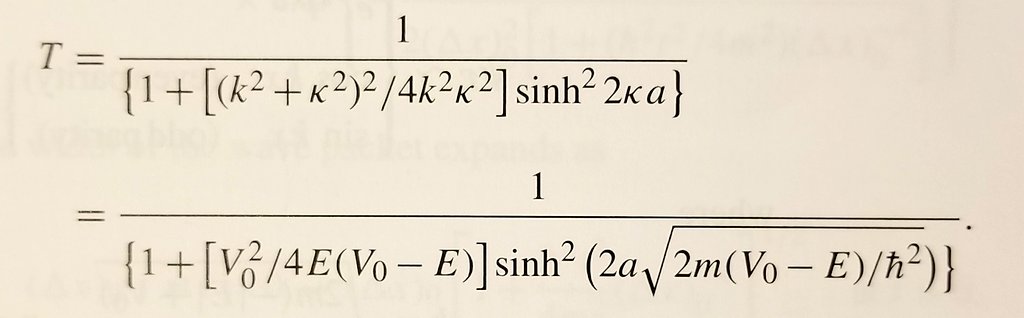
V: energy of potential barrier
E: energy of particle
a: width of barrier
m: mass of particle
ћ (or h_bar): Planck constant divided by 2π (just a constant we need in quantum).
Sinh is the hyperbolic sine function that absorbs the imaginary part of sin